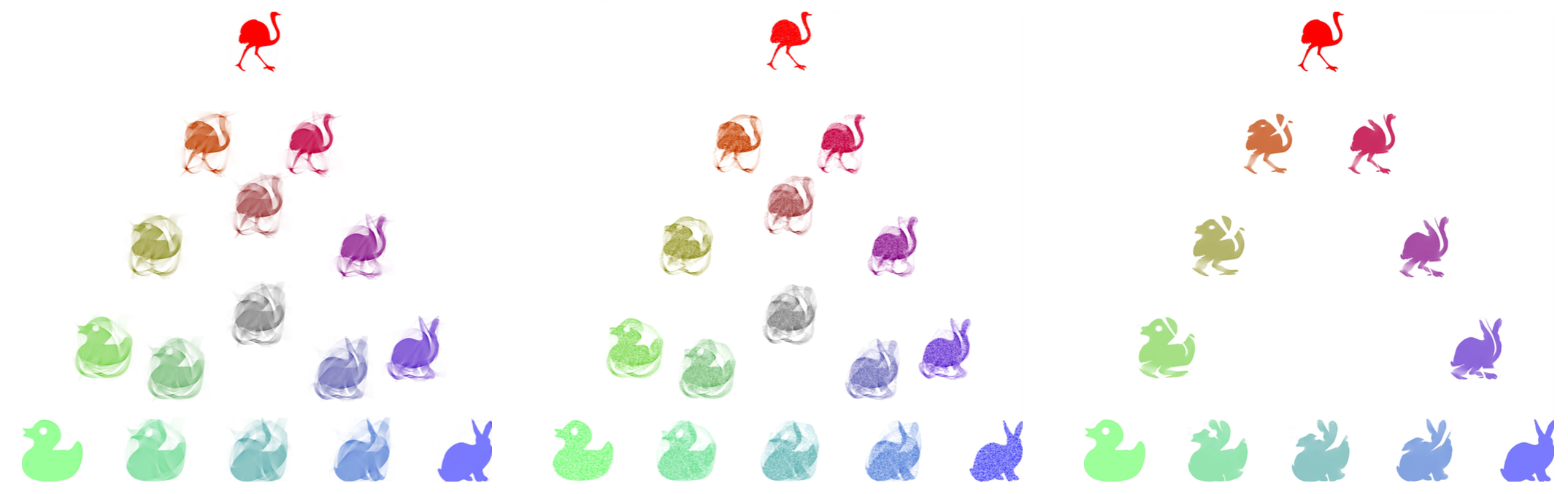
Sliced and Radon Wasserstein Barycenters of Measures
Journal of Mathematical Imaging and Vision, 2014.
This article details two approaches to compute barycenters of measures using 1-D Wasserstein distances along radial projections of the input measures. The first method makes use of the Radon transform of the measures, and the second is the solution of a convex optimization problem over the space of measures. We show several properties of these barycenters and explain their relationship. We show numerical approximation schemes based on a discrete Radon transform and on the resolution of a non-convex optimization problem. We explore the respective merits and drawbacks of each approach on applications to two image processing problems: color transfer and texture mixing.