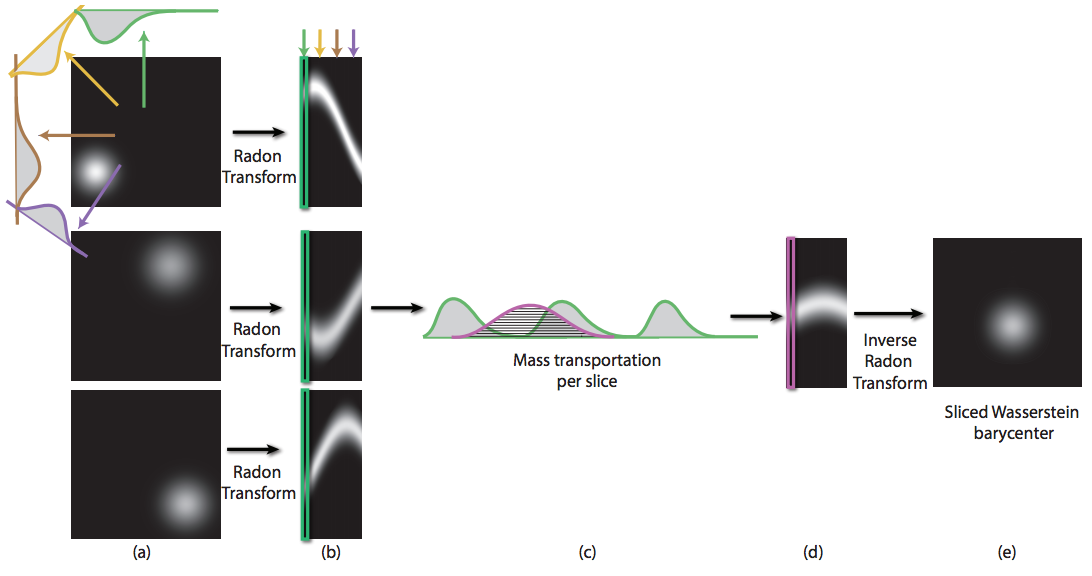
The optimal mass transportation problem provides a framework for interpolating between different probability density functions (pdfs), warping one function toward another. Interpolating between two arbitrary pdfs can be challenging, but interpolating between more than two pdfs just remains untractable. We propose an approximation of such interpolations based on 1D projections, that is efficiently solved via Radon transforms. We observe the expected translational behavior of this interpolation on smooth 2D functions, and prove that it corresponds to the exact interpolant in a few particular cases.